Version: 14

viktor.geometry

Arc

class viktor.geometry.Arc(centre_point, start_point, end_point, short_arc=True, *, n_segments=30, color=(0, 0, 0), identifier=None)

Bases: TransformableObject

Creates a constant radius arc in the xy plane. Clockwise rotation creates an outward surface.

Parameters:

centre_point (Union[Point, Tuple[float, float, float]]) – Point in xy plane.
start_point (Union[Point, Tuple[float, float, float]]) – Point in xy plane. Should have the same distance to centre_point as end_point.
end_point (Union[Point, Tuple[float, float, float]]) – Point in xy plane. Should have the same distance to centre_point as start_point.
short_arc (bool) – Angle of arc smaller than pi if True, larger than pi if False.
n_segments (int) – Number of discrete segments of the arc (default: 30)
New in v13.5.0
.
color (Color) – Visualization color
New in v13.5.0
.
identifier (str) – object identifier (new in v14.10.0)

property angle: float: Absolute angle of the arc in radians, which is the difference between theta1 and theta2.

property centre_point: Point

discretize(num=2)

Returns a discrete representation of the arc, as a list of Point objects. The amount of points can be specified using ‘num’, which should be larger than 1.

Return type:: List[Point]

property end_point: Point

property length: float: Arc length.

property n_segments: int

property radius: float

revolve(*, rotation_angle=None, material=None, identifier=None, **kwargs)

Returns an ArcRevolve object, revolved around the global y-axis.

Parameters:

rotation_angle (float) – Angle of the revolved object according to the right-hand-rule, with the start of the rotation in positive z-direction. Angle in radians. If not specified, 2 pi will be used.
material (Material) – optional material
identifier (str) – object identifier (new in v14.10.0)

Return type:

ArcRevolve

property short_arc: bool

property start_point: Point

property theta1: float: Angle of the end point with respect to the x-axis in radians.

property theta1_theta2: Tuple[float, float]: Angles of the end (theta1) and start (theta2) points with respect to the x-axis in radians.

property theta2: float: Angle of the start point with respect to the x-axis in radians.

ArcExtrusion

class viktor.geometry.ArcExtrusion(profile, arc, profile_rotation=0, n_segments=50, *, material=None, identifier=None)

Bases: Group

Given an Arc and a cross-section of the extrusion, a discretized Extrusion object is returned.

The coordinates of the profile are defined with respect to the Arc and have a LOCAL coordinate system:

z-axis is in direction of the arc from start to end.

x-axis is in positive global z-axis.

y-axis follows from the right-hand-rule.

Rotation of the profile is about the axis according to the right-hand-rule with LOCAL z-axis (see definition above).

Example:

profile = [
    Point(1, 1),
    Point(1, 2),
    Point(3, 2),
    Point(3, 1),
    Point(1, 1),
]
arc = Arc(Point(1, 1, 0), Point(3, 1, 0), Point(1, 3, 0))
arc_ext = ArcExtrusion(profile, arc, profile_rotation=10, n_segments=10)

This will result in the following visualization, where the Arc itself is also shown in the xy plane:

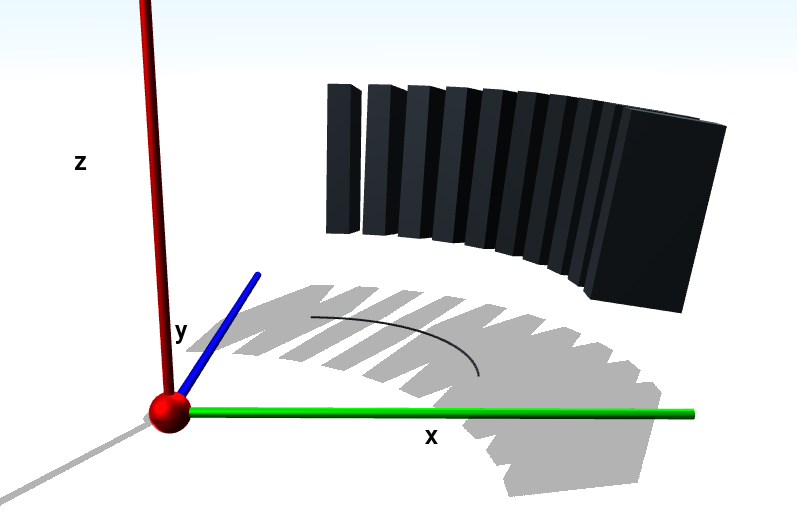
Parameters:

profile (List[Point]) – Coordinates of cross-section.
arc (Arc) – An Arc object is used to define the direction of the extrusion.
profile_rotation (float) – Rotation of the profile around its local Z-axis in degrees.
n_segments (int) – Number of discrete segments of the arc, which is 50 by default.
material (Material) – optional material
identifier (str) – object identifier (new in v14.10.0)

ArcRevolve

class viktor.geometry.ArcRevolve(arc, *args, rotation_angle=None, material=None, identifier=None, **kwargs)

Bases: Revolve

Returns a revolved object of an arc around the global y-axis.

In the example below, rotation_angle is equal to pi / 3:

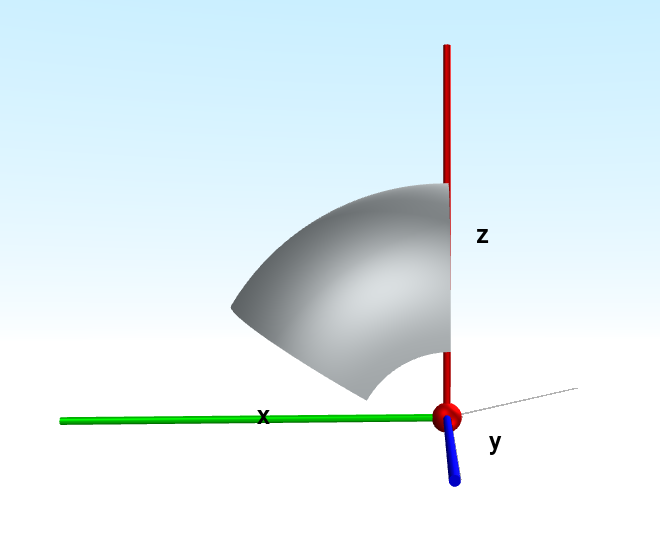
Parameters:

arc (Arc) – Arc object.
rotation_angle (float) – Angle of the revolved object according to the right-hand-rule, with the start of the rotation in positive z-direction. Angle in radians. If not specified, 2 pi will be used.
material (Material) – optional material
identifier (str) – object identifier (new in v14.10.0)

property arc: Arc: Arc

property height: float: Height of the object.

property inner_volume: float

Returns the inner volume of the revolved object.

This method will only return a value if the defined Arc meets the following conditions:

it should be short, i.e. short_arc=True

the start- and end-point are located on the same side w.r.t. the y-axis of the center-point of the Arc

it is defined in clockwise direction

property surface_area: float: Total exterior area of the object.

property uuid: str

BidirectionalPattern

class viktor.geometry.BidirectionalPattern(base_object, direction_1, direction_2, number_of_elements_1, number_of_elements_2, spacing_1, spacing_2, *, identifier=None)

Bases: Pattern

Instantiates a two-dimensional pattern, evenly spaced in two separate directions. If identifier has been set on the base-object, the identifiers of the objects within the pattern are suffixed with ‘-i’ (i = 1, 2, 3, …).

Parameters:

base_object (TransformableObject) – the object to be duplicated
direction_1 (List[float]) – a unit vector specifying the first direction
direction_2 (List[float]) – a unit vector specifying the second direction
number_of_elements_1 (int) – total amount of elements along direction 1
number_of_elements_2 (int) – total amount of elements along direction 2
spacing_1 (float) – the applied spacing in direction 1
spacing_2 (float) – the applied spacing in direction 2
identifier (str) – object identifier (new in v14.10.0)

CartesianAxes

class viktor.geometry.CartesianAxes(origin=Point(0.000e+00, 0.000e+00, 0.000e+00), axis_length=1, axis_diameter=0.05)

Bases: Group

Helper visualisation object to show positive x (red), y (green) and z (blue) axes.

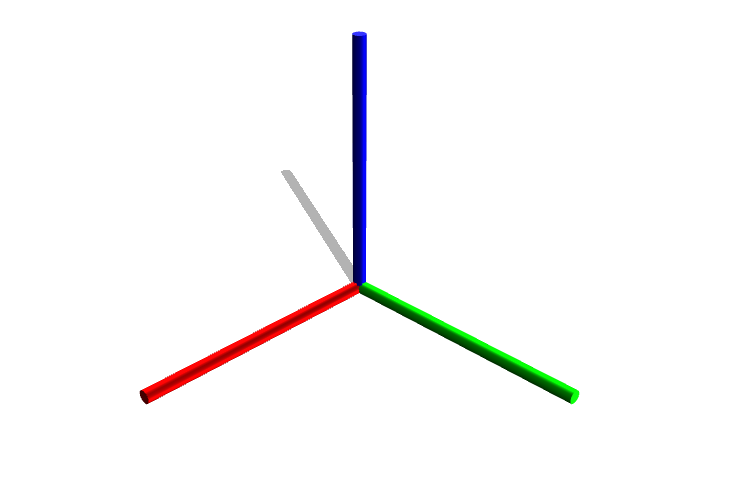
Parameters:

origin (Point) – Coordinates of the origin.
axis_length (float) – Length of the axes.
axis_diameter (float) – Diameter of the axes.

CircularExtrusion

class viktor.geometry.CircularExtrusion(diameter, line, *, shell_thickness=None, material=None, identifier=None)

Bases: TransformableObject

This class is used to construct an extrusion which has a circular base, e.g. a circular foundation pile.

Parameters:

diameter (float) – Outer diameter of the cross-section.
line (Line) – Line object along which the circular cross-section is extruded.
shell_thickness (float) – Optional shell thickness. None for solid (default: None)
New in v13.6.0
.
material (Material) – Optional material.
identifier (str) – object identifier (new in v14.10.0)

property cross_sectional_area: float

property diameter: float

property length: float

property line: Line

property radius: float

property shell_thickness: float | None

Cone

class viktor.geometry.Cone(diameter, height, *, origin=None, orientation=None, material=None, identifier=None)

Bases: TransformableObject

Creates a cone object.

Parameters:

diameter (float) – Diameter of the circular base surface.
height (float) – Height from base to tip.
origin (Point) – Optional location of the centroid of the base surface (default: Point(0, 0, 0)).
orientation (Vector) – Optional orientation from origin to the tip (default: Vector(0, 0, 1)).
material (Material) – Optional material.
identifier (str) – object identifier (new in v14.10.0)

classmethod from_line(diameter, line, *, material=None, identifier=None)

Create a Cone object by a given base diameter and line.

Parameters:

diameter (float) – Diameter of the circular base surface.
line (Line) – Line from base to top of the cone. The start point of the line represents the location of the center of the base, and the end point represents the tip of the cone.
material (Material) – Optional material.
identifier (str) – object identifier (new in v14.10.0)

Return type:

Cone

Extrusion

class viktor.geometry.Extrusion(profile, line, profile_rotation=0, *, material=None, identifier=None)

Bases: Group

Extruded object from a given set of points, which is called the profile. This profile should meet the following requirements:

start point should be added at the end for closed profile

points should be defined in z=0 plane

circumference should be defined clockwise

Note that the profile is defined with respect to the start point of the Line object, i.e. the profile is defined in the local coordinate system. An example is given below of two extrusions with the same dimensions. Their corresponding Line objects are also visualized. The extrusion have the following profile:

# black box
profile_b = [
    Point(1, 1),
    Point(1, 2),
    Point(2, 2),
    Point(2, 1),
    Point(1, 1),
]
box_b = Extrusion(profile_b, Line(Point(4, 1, 0), Point(4, 1, 1)))

# yellow box
profile_y = [
    Point(-0.5, -0.5),
    Point(-0.5, 0.5),
    Point(0.5, 0.5),
    Point(0.5, -0.5),
    Point(-0.5, -0.5),
]
box_y = Extrusion(profile_y, Line(Point(2, 2, 0), Point(2, 2, 1)))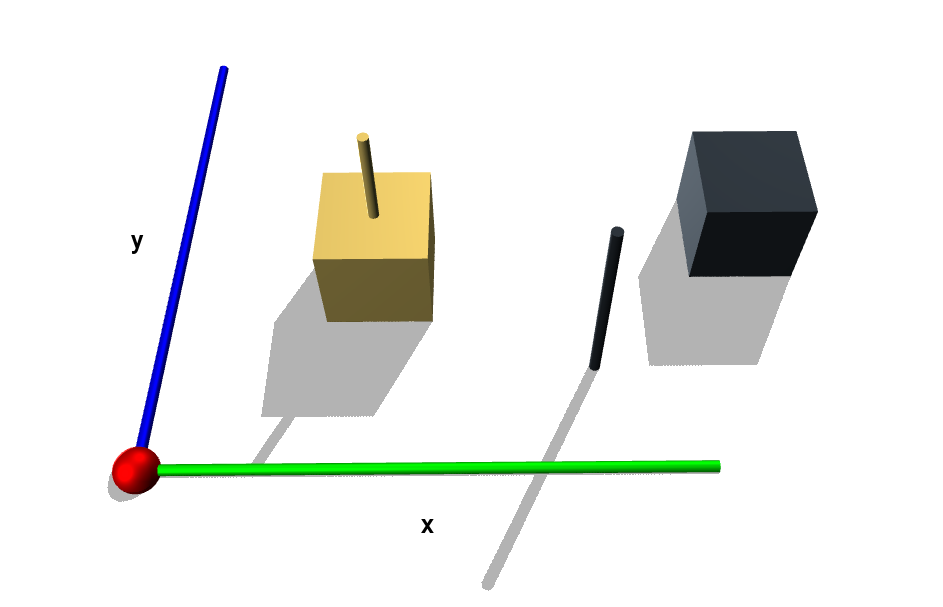

Parameters:

profile (List[Point]) – Coordinates of cross-section.
line (Line) – A line object is used to define the length (thickness) of the extrusion.
profile_rotation (float) – Rotation of the profile around the Z-axis in degrees.
material (Material) – optional material
identifier (str) – object identifier (new in v14.10.0)

property length: float

property line: Line

property material: Material

property profile: List[Point]

GeoPoint

class viktor.geometry.GeoPoint(lat, lon)

Geographical point on the Earth’s surface described by a latitude / longitude coordinate pair.

This object can be created directly, or will be returned in the params when using a GeoPointField.

Parameters:

lat (float) – Latitude, between -90 and 90 degrees.
lon (float) – Longitude, between -180 and 180 degrees.

classmethod from_rd(coords)

Instantiates a GeoPoint from the provided RD coordinates.

Parameters:: coords (Tuple[float, float]) – RD coordinates (x, y).
Return type:: GeoPoint

property rd: Tuple[float, float]: RD representation (x, y) of the GeoPoint.

GeoPolygon

class viktor.geometry.GeoPolygon(*points)

Geographical polygon on the Earth’s surface described by a list of GeoPoints.

This object can be created directly, or will be returned in the params when using a GeoPolygonField.

Parameters:: points (GeoPoint) – Geo points (minimum 3). The profile is automatically closed, so it is not necessary to add the start point at the end.

property points: List[GeoPoint]

GeoPolyline

class viktor.geometry.GeoPolyline(*points)

Geographical polyline on the Earth’s surface described by a list of GeoPoints.

This object can be created directly, or will be returned in the params when using a GeoPolylineField.

Parameters:: points (GeoPoint) – Geo points (minimum 2).

property points: List[GeoPoint]

Group

class viktor.geometry.Group(objects, *, identifier=None)

Bases: TransformableObject

Parameters:

objects (Sequence[TransformableObject]) – Objects that are part of the group.
identifier (str) – object identifier (new in v14.10.0)

add(objects)

Return type:: None

property children: List[TransformableObject]

duplicate()

Return type:: Group

Line

class viktor.geometry.Line(start_point, end_point, *, color=(0, 0, 0), identifier=None)

Bases: TransformableObject

Parameters:

start_point (Union[Point, Tuple[float, float, float]]) – Start point of the line (cannot coincide with end_point).
end_point (Union[Point, Tuple[float, float, float]]) – End point of the line (cannot coincide with start_point).
color (Color) – Visualization color
New in v13.5.0
.
identifier (str) – object identifier (new in v14.10.0)

collinear(point)

True if point is collinear (in line) with Line, else False.

Return type:: bool

direction(normalize=True)

Direction vector between start and end point.

Return type:: Vector

distance_to_point(point)

Calculate the (minimal) distance from the given point to the (unbounded) line.

Return type:: float

property end_point: Point

find_overlap(other, inclusive=False)

Find the overlapping part of this line with another line.

The returned value depends on the situation:

None, if no overlap is found or the two lines are not parallel
Point, if an overlap is found with length equal to 0
Line, if an overlap is found with length larger than 0

Parameters:

other (Line) – Other Line object
inclusive (bool) – True to treat overlapping points as overlap

Return type:

Union[Point, Line, None]

get_line_function_parameters()

Get parameters for y=ax+b definition of a line.

Return type:: Tuple[float, float]
Returns:: (a, b) or (nan, nan) if line is vertical

property horizontal: bool

property length: float

property length_vector: numpy.ndarray

project_point(point)

Project the point on the (unbounded) line.

Return type:: Point

revolve(*, material=None, identifier=None, **kwargs)

Revolve line around y-axis, only possible for lines in x-y plane.

Parameters:

material (Material) – optional material
identifier (str) – object identifier (new in v14.10.0)

Raises:

NotImplementedError – when line is not in x-y plane

Return type:

LineRevolve

property start_point: Point

property unit_vector: numpy.ndarray

property vertical: bool

LineRevolve

class viktor.geometry.LineRevolve(line, *args, material=None, identifier=None, **kwargs)

Bases: Revolve

Returns a revolved object of a Line around the global y-axis.

An example revolve of a line between the point (1, 1, 0) and (3, 2, 0) is shown below, with the line object shown in black.

line = Line(Point(1, 1, 0), Point(3, 2, 0))
line_rev = LineRevolve(line)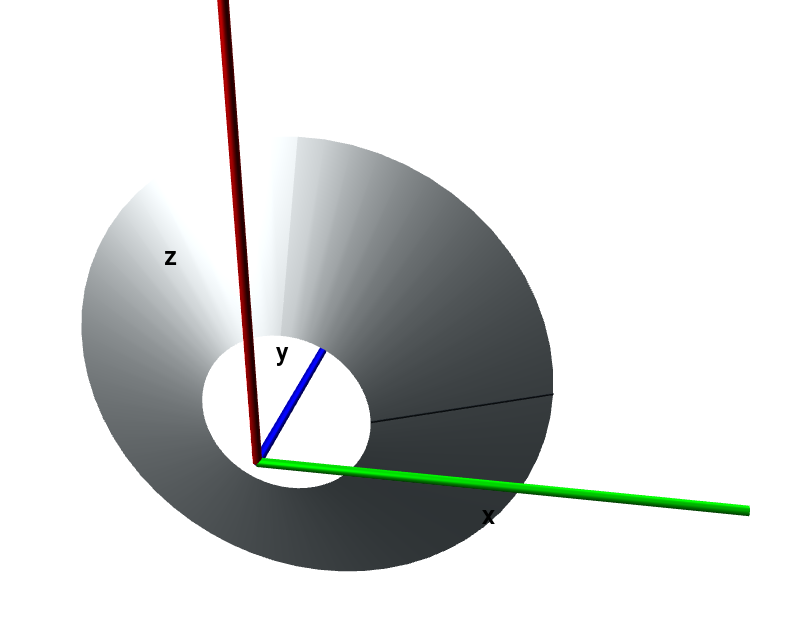

Parameters:

line (Line) – Line object which is to be revolved.
material (Material) – optional material
identifier (str) – object identifier (new in v14.10.0)

property height: float

property inner_volume: float

Returns the inner volume of the revolved object.

This method will only return a value if the defined Line meets the following conditions:

it should NOT be horizontal, i.e. y_start != y_end

it should be defined in positive y-direction, i.e. y_start < y_end

property line: Line

property surface_area: float: Returns the total exterior area of the revolved object.

property uuid: UUID

LinearPattern

class viktor.geometry.LinearPattern(base_object, direction, number_of_elements, spacing, *, identifier=None)

Bases: Pattern

Instantiates a linear, evenly spaced, pattern along a single direction. If identifier has been set on the base-object, the identifiers of the objects within the pattern are suffixed with ‘-i’ (i = 1, 2, 3, …).

Parameters:

base_object (TransformableObject) – the object to be duplicated
direction (List[float]) – a unit vector specifying in which direction the pattern propagates
number_of_elements (int) – total amount of elements in the pattern, including the base object
spacing (float) – the applied spacing
identifier (str) – object identifier (new in v14.10.0)

Material

class viktor.geometry.Material(name=None, density=None, price=None, *, threejs_type='MeshStandardMaterial', roughness=1.0, metalness=0.5, opacity=1.0, color=(221, 221, 221))

Note

The following properties were renamed since v14.5.0. If you are using a lower version, please use the old naming.

threejs_roughness -> roughness
threejs_metalness -> metalness
threejs_opacity -> opacity

Parameters:

name (str) – Optional name.
density (float) – Optional density.
price (float) – Optional price.
threejs_type (str) – deprecated
roughness (float) – Between 0 - 1 where closer to 1 gives the material a rough texture.
metalness (float) – Between 0 - 1 where closer to 1 gives the material a shiny metal look.
opacity (float) – Between 0 - 1 where closer to 0 makes the material less visible.
color (Color) – Color of the material.

Pattern

class viktor.geometry.Pattern(base_object, duplicate_translation_list, *, identifier=None)

Bases: Group

Instantiates a pattern based on a base object and several duplicates, each translated by an input vector. If identifier has been set on the base-object, the identifiers of the objects within the pattern are suffixed with ‘-i’ (i = 1, 2, 3, …).

Parameters:

base_object (TransformableObject) – the object to be duplicated
duplicate_translation_list (List[List[float]]) – a list of translation vectors, each of which generates a duplicate
identifier (str) – object identifier (new in v14.10.0)

Point

class viktor.geometry.Point(x, y, z=0)

This class represents a point object, which is instantiated by means of 3-dimensional coordinates X, Y, and Z. It forms a basis of many structural 2D and 3D objects.

Example usage:

p1 = Point(1, 2)        # create a 2D point
p1.z                    # 0
p2 = Point(1, 2, 3)     # create a 3D point
p1.z                    # 3

Parameters:

x (float) – X-coordinate.
y (float) – Y-coordinate.
z (float) – (optional) Z-coordinate, defaults to 0.

Raises:

TypeError – if the point is instantiated with a None value.

coincides_with(other)

Given another Point object, this method determines whether the two points coincide.

Return type:: bool

property coordinates: numpy.ndarray: Coordinates of the Point as array (X, Y, Z).

copy()

Returns a deep copy of the object.

Return type:: Point

get_local_coordinates(local_origin, spherical=False)

Method to determine the local coordinates of the current Point with respect to a ‘local origin’.

Return type:: ndarray

vector_to(point)

Vector pointing from self to point.

Example usage:

p1 = Point(1, 2, 3)
p2 = Point(0, 0, 0)         # origin
v = p1.vector_to(p2)        # vector from p1 to the origin
v = p1.vector_to((0, 0, 0)) # short notation

Return type:: Vector

property x: float: X-coordinate.

property y: float: Y-coordinate.

property z: float: Z-coordinate.

Polygon

class viktor.geometry.Polygon(points, *, surface_orientation=False, material=None, skip_duplicate_vertices_check=False, identifier=None)

Bases: TransformableObject

2D closed polygon without holes in x-y plane.

Parameters:

points (List[Point]) – profile is automatically closed, do not add start point at the end. only the x and y coordinates are considered. left hand rule around circumference determines surface direction
surface_orientation (bool) –
- if True, the left hand rule around circumference determines surface direction
- if False, surface always in +z direction
material (Material) – optional material
skip_duplicate_vertices_check (bool) – if True, duplicate vertices are not filtered on serialization of the triangles. This may boost performance (default: False).
identifier (str) – object identifier (new in v14.10.0)

Raises:

ValueError –

if less than 3 points are provided.
if points contains duplicates.
if points form a polygon with self-intersecting lines.
if points are all collinear.

property centroid: Tuple[float, float]: Returns the centroid (X, Y) of the polygon.

property cross_sectional_area: float

extrude(line, *, profile_rotation=0, material=None, identifier=None)

Extrude the Polygon in the direction of the given line. Polygon must be defined in clockwise direction.

Parameters:

line (Line) – A line object is used to define the length (thickness) of the extrusion.
profile_rotation (float) – Rotation of the profile around the Z-axis in degrees.
material (Material) – optional material
identifier (str) – object identifier (new in v14.10.0)

Raises:

ValueError – if polygon is defined in anti-clockwise direction

Return type:

Extrusion

has_clockwise_circumference()

Return type:: bool

Method determines the direction of the input points, and returns:

True if the circumference is clockwise
False if the circumference is counter-clockwise

property moment_of_inertia: Tuple[float, float]: Returns the moment of inertia (Ix, Iy) in xy-plane.

Polyline

class viktor.geometry.Polyline(points, *, color=(0, 0, 0), identifier=None)

Bases: TransformableObject

Representation of a polyline made up of multiple straight line segments.

This class is immutable, meaning that all functions that perform changes on a polyline will return a mutated copy of the original polyline.

Parameters:

points (List[Point]) – List of points, which may contain duplicate points. Note that when calling the individual lines of the polyline, duplicate points are filtered (i.e. zero-length lines are omitted).
color (Color) – Visualization color
New in v13.5.0
.
identifier (str) – object identifier (new in v14.10.0)

combine_with(other)

Given two polylines that have at least one point in common and together form one line without any side branches, combine those two polylines. The combined line will contain all points of both polylines.

Parameters:: other (Polyline)
Return type:: Polyline

property end_point: Point: Last point in polyline.points

filter_duplicate_points()

Returns a new Polyline object. If two consecutive points in this polyline coincide, the second point will be omitted

Return type:: Polyline

find_overlaps(other)

Find all overlapping regions of this polyline with another polyline. The returned overlapping regions will all point in the direction of this line. The overlap polylines will contain all points of both polylines, even if they only occur in one of the lines.

If no overlaps are found, an empty list will be returned.

Parameters:: other (Polyline)
Return type:: List[Polyline]

classmethod from_lines(lines)

Create a polyline object from a list of lines.

The end of one line must always coincide with the start of the next line.

Parameters:: lines (Sequence[Line]) – Sequence of lines
Return type:: Polyline

classmethod get_lowest_or_highest_profile_x(profile_1, profile_2, lowest)

Given two polylines with n intersections, return a third polyline that will always follow the lowest (or highest) of the two lines the x locations of the points of the two polylines should be not descending (lines from left to right or vertical) the returned polyline will only cover the overlapping range in x coordinates.

If one of the profiles is an empty polyline, an empty polyline will be returned.

examples:

                                   /----------------|
                                  /         /-------|--------------------
profile_1: ----------------\     /         /        |
                            \   /         /         |_____________________________
profile_2:      -------------\-/         /
                              \_________/

get_lowest_or_highest_profile_x(cls, profile_1, profile_2, lowest=True) will return:


                                           /-------|
                                          /        |
                                         /         |____________________
   result:     -------------\           /
                             \_________/

Note that only the overlapping region of the two profiles is returned!

Parameters:

profile_1 (Polyline)
profile_2 (Polyline)
lowest (bool) – switch to decide whether to return highest or lowest profile

Return type:

Polyline

Currently, this implementation is exclusive. Meaning that vertical line parts that lie on the start or end of the overlap region in x are not taken into account.

get_polyline_between(start_point, end_point, inclusive=False)

Given two points that both lie on a polyline, return the polyline that lies between those two points start_point has to lie before end_point on this polyline.

If the given start point lies after the given end point on this polyline, an empty polyline will be returned. If the two given points are identical, it depends on the inclusive flag whether a polyline containing that point once, or an empty polyline will be returned.

Parameters:

start_point (Point)
end_point (Point)
inclusive (bool) – if true, the start and the end points will be added to the returned list

Raises:

ValueError – when one of the two given points does not lie on this polyline

Return type:

Polyline

get_reversed_polyline()

Returns a polyline that is the reverse of this one.

Return type:: Polyline

intersections_with_polyline(other_polyline)

Find all intersections with another polyline and return them ordered according to the direction of this polyline

If the polylines are partly parallel, the start and end points of the parallel section will be returned as intersections. If one of the polylines is a subset of the other, or the two lines are completely parallel, no intersections will be found.

Parameters:: other_polyline (Polyline)
Return type:: List[Point]

intersections_with_x_location(x)

Find all intersections of this polyline with a given x location. Ordered from start to end of this polyline.

If this line is partly vertical, the start and end points of the vertical section will be returned as an intersection. If this line is completely vertical, no intersections will be found.

Parameters:: x (float)
Return type:: List[Point]

is_equal_to(other)

Check if all points in this polyline coincide with all points of another polyline

Parameters:: other (Polyline) – Other polyline
Return type:: bool

is_monotonic_ascending_x(strict=True)

Check if the x coordinates of the points of this polyline are ascending.

Parameters:: strict (bool) – when set to false, equal x coordinates are accepted between points
Return type:: bool

is_monotonic_ascending_y(strict=True)

Check if the y coordinates of the points of this polyline are ascending

Parameters:: strict (bool) – when set to false, equal y coordinates are accepted between points
Return type:: bool

property lines: List[Line]: A list of lines connecting all polyline points. Lines between coincident points are skipped.

point_is_on_polyline(point)

Check if a given point lies on this polyline

Parameters:: point (Point)
Return type:: bool

property points: List[Point]

serialize()

Return a json serializable dict of form:

[
    {'x': point_1.x, 'y': point_1.y},
    {'x': point_2.x, 'y': point_2.y}
]

Return type:: List[dict]

split(point)

return the two separate parts of this polyline before and after the given point.

Parameters:: point (Point)
Raises:: ValueError – if the provided point does not lie on this polyline.
Return type:: Tuple[Polyline, Polyline]

property start_point: Point: First point in polyline.points

property x_max: float | None: The highest x-coordinate present within this polyline.

property x_min: float | None: The lowest x-coordinate present within this polyline.

property y_max: float | None: The highest y-coordinate present within this polyline.

property y_min: float | None: The lowest y-coordinate present within this polyline.

property z_max: float | None: The highest z-coordinate present within this polyline.

property z_min: float | None: The lowest z-coordinate present within this polyline.

RDWGSConverter

class viktor.geometry.RDWGSConverter

Class that provides functions to translate latitude and longitude coordinates between the WGS system and RD system.

The RD coordinate system is a cartesian coordinate system that is frequently used for in civil engineering to describe locations in the Netherlands. The origin is located in france, so that for all of the Netherlands, both x (m) and y (m) values are positive and y is always larger then x. The domain in which the RD coordinate system is valid is:

x: [-7000, 300000]
y: [289000, 629000]

About the RD coordinate system: https://nl.wikipedia.org/wiki/Rijksdriehoeksco%C3%B6rdinaten

X0 = 155000

Y0 = 463000

static from_rd_to_wgs(coords)

Convert RD coordinates (x, y) to WGS coordinates [latitude, longitude].

lat, lon = RDWGSConverter.from_rd_to_wgs((100000, 400000))

Parameters:: coords (Tuple[float, float]) – RD coordinates (x, y)
Return type:: List[float]

static from_wgs_to_rd(coords)

Convert WGS coordinates (latitude, longitude) to RD coordinates [x, y].

x, y = RDWGSConverter.from_wgs_to_rd((51.58622, 4.59360))

Parameters:: coords (Tuple[float, float]) – WGS coordinates (latitude, longitude)
Return type:: List[float]

lam0 = 5.38720621

phi0 = 52.1551744

RectangularExtrusion

class viktor.geometry.RectangularExtrusion(width, height, line, profile_rotation=0, *, material=None, identifier=None)

Bases: Extrusion

Extruded object from a given set of points, which is called the profile. This profile should meet the following requirements:

start point should be added at the end for closed profile

points should be defined in z=0 plane

circumference should be defined clockwise

# black box
profile_b = [
    Point(1, 1),
    Point(1, 2),
    Point(2, 2),
    Point(2, 1),
    Point(1, 1),
]
box_b = Extrusion(profile_b, Line(Point(4, 1, 0), Point(4, 1, 1)))

# yellow box
profile_y = [
    Point(-0.5, -0.5),
    Point(-0.5, 0.5),
    Point(0.5, 0.5),
    Point(0.5, -0.5),
    Point(-0.5, -0.5),
]
box_y = Extrusion(profile_y, Line(Point(2, 2, 0), Point(2, 2, 1)))

Parameters:

profile – Coordinates of cross-section.
line (Line) – A line object is used to define the length (thickness) of the extrusion.
profile_rotation (float) – Rotation of the profile around the Z-axis in degrees.
material (Material) – optional material
identifier (str) – object identifier (new in v14.10.0)

property cross_sectional_area: float: Returns the area of the cross-section (width x height).

property height: float: Height of the extrusion.

property inner_volume: float: Returns the inner volume of the extruded object.

property width: float: Width of the extrusion.

Revolve

class viktor.geometry.Revolve(*args, rotation_angle=None, material=None, identifier=None, **kwargs)

Bases: TransformableObject, ABC

Abstract base class of a revolved object.

abstract property inner_volume: float

property mass: float: Calculates the mass of the object as rho * area * thickness, with rho the density of the Material.

abstract property surface_area: float

property thickness: float

Sphere

class viktor.geometry.Sphere(centre_point, radius, width_segments=30, height_segments=30, material=None, *, identifier=None)

Bases: TransformableObject

This class can be used to construct a spherical object around the specified coordinate.

The smoothness of the edges can be altered by setting width_segments and height_segments. In the example below both the default smoothness of 30 (left) and a rough sphere with 5 segments (right) is shown:

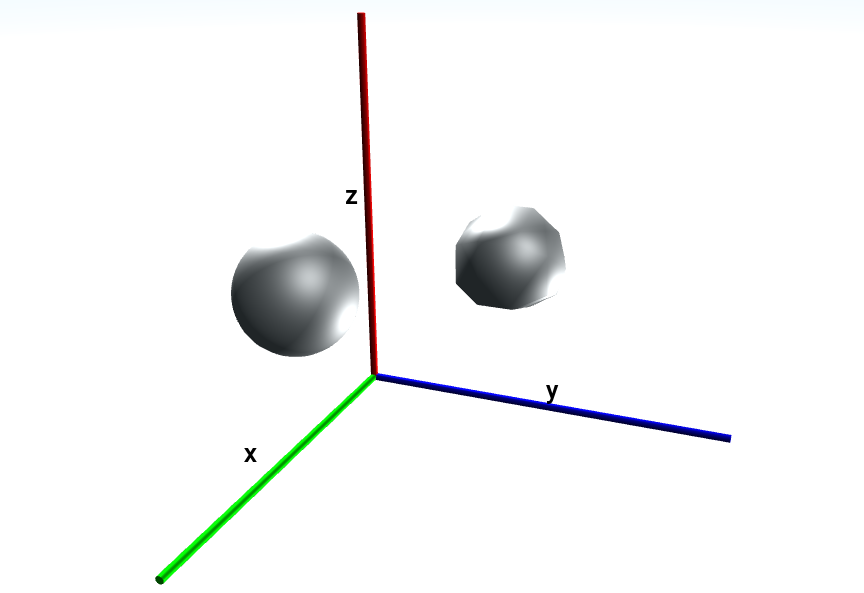
Parameters:

centre_point (Point) – Center point of the sphere.
radius (float) – Radius of the sphere.
width_segments (float) – Sets the smoothness in xz-plane.
height_segments (float) – Sets the smoothness in yz-plane.
material (Material) – Optionally a custom material can be set.
identifier (str) – object identifier (new in v14.10.0)

circumference()

Return type:: float

diameter()

Return type:: float

surface_area()

Return type:: float

volume()

Return type:: float

SquareBeam

class viktor.geometry.SquareBeam(length_x, length_y, length_z, *, material=None, identifier=None)

Bases: RectangularExtrusion

High level object to create a rectangular beam object around the origin. The centroid of the beam is located at the origin (0, 0, 0).

Parameters:

length_x (float) – Width of the extrusion in x-direction.
length_y (float) – Length of the extrusion in y-direction.
length_z (float) – Height of the extrusion in z-direction.
material (Material) – optional material
identifier (str) – object identifier (new in v14.10.0)

Torus

class viktor.geometry.Torus(radius_cross_section, radius_rotation_axis, rotation_angle=6.283185307179586, *, material=None, identifier=None)

Bases: Group

Create a torus object

Parameters:

radius_cross_section (float)
radius_rotation_axis (float) – measured from central axis to centre of cross-section.
rotation_angle (float) – optional argument to control how large of a torus section you want. 2pi for complete torus
material (Material) – optional material
identifier (str) – object identifier (new in v14.10.0)

property inner_volume: float

property material: Material

TransformableObject

class viktor.geometry.TransformableObject(*, identifier=None)

Bases: ABC

mirror(point, normal)

Mirror an object on a plane defined by a point and normal vector.

Parameters:

point (Union[Point, Tuple[float, float, float]]) – Point within the mirror plane.
normal (Union[Vector, Tuple[float, float, float]]) – Normal vector of the mirror plane.

Return type:

TransformableObject

rotate(angle, direction, point=None)

Rotate an object along an axis (direction) by an angle. Direction will follow right hand rule.

Parameters:

angle (float) – Angle of desired rotation in radians.
direction (Union[Vector, Tuple[float, float, float]]) – Vector along which rotation is to be performed.
point (Union[Point, Tuple[float, float, float]]) – Point through which the rotation vector runs.

Return type:

TransformableObject

scale(scaling_vector)

Scale an object along a scaling vector.

Parameters:: scaling_vector (Union[Vector, Tuple[float, float, float]]) – Vector along which scaling is to be performed.
Return type:: TransformableObject

translate(translation_vector)

Translate an object along a translation vector.

Parameters:: translation_vector (Union[Vector, Tuple[float, float, float]]) – Vector along which translation is to be performed.
Return type:: TransformableObject

Triangle

class viktor.geometry.Triangle(point1, point2, point3)

Creates a Triangle object from 3D vertices.

Parameters:

point1 (Point) – First vertex.
point2 (Point) – Second vertex.
point3 (Point) – Third vertex.

area()

Returns the area of the triangle.

Return type:: float

property centroid: Tuple[float, float, float]: Returns the centroid (X, Y, Z) of the triangle.

property moment_of_inertia: Tuple[float, float]: Returns the moment of inertia (Ix, Iy) (only in x-y plane).

TriangleAssembly

class viktor.geometry.TriangleAssembly(triangles, *, material=None, skip_duplicate_vertices_check=False, identifier=None)

Bases: TransformableObject

Fundamental visualisation geometry, built up from triangles. Right hand rule on triangle circumference determines the surface direction.

Parameters:

triangles (List[Triangle]) – Triangles of the assembly.
material (Material) – optional material.
skip_duplicate_vertices_check (bool) – if True, duplicate vertices are not filtered on serialization of the triangles. This may boost performance (default: False).
identifier (str) – object identifier (new in v14.10.0)

Vector

class viktor.geometry.Vector(x, y, z=0)

A 3-dimensional vector in space.

The following operations are supported:

Negation

v1 = Vector(1, 2, 3)
v2 = -v1  # results in Vector(-1, -2, -3)

Addition

v1 = Vector(1, 2, 3)
v2 = Vector(1, 2, 3)
v3 = v1 + v2  # results in Vector(2, 4, 6)

Subtraction

v1 = Vector(1, 2, 3)
v2 = Vector(1, 2, 3)
v3 = v1 - v2  # results in Vector(0, 0, 0)

(reverse) Multiplication

v1 = Vector(1, 2, 3)
v2 = v1 * 3  # results in Vector(3, 6, 9)
v3 = 3 * v1  # results in Vector(3, 6, 9)

Dot product

v1 = Vector(1, 2, 3)
v2 = Vector(1, 2, 3)
res = v1.dot(v2)  # results in 14

Cross product

v1 = Vector(1, 0, 0)
v2 = Vector(0, 1, 0)
v3 = v1.cross(v2)  # results in Vector(0, 0, 1)

Parameters:

x (float) – X-coordinate.
y (float) – Y-coordinate.
z (float) – Z-coordinate (default: 0).

property coordinates: Tuple[float, float, float]: Coordinates of the Vector as tuple (X, Y, Z).

cross(other)

Vector product of two vectors.

Parameters:: other (Vector) – Second Vector
Return type:: Vector

dot(other)

Scalar product of two vectors.

Parameters:: other (Vector) – Second Vector
Return type:: float

property magnitude: float: Magnitude of the Vector.

normalize()

Return the normalized vector (with unit-length).

Raises:: ValueError – if vector is a null-vector.
Return type:: Vector

property squared_magnitude: float: Vector magnitude without square root; faster than magnitude.

add_point

viktor.geometry.add_point(unique_points, point)

Adds a Point object to a unique list of Point objects. The point is only added when not already present in the list.

Parameters:

unique_points (List[Point]) – List of point objects.
point (Point) – Point object which has to be added.

Return type:

Tuple[List[Point], int]

calculate_distance_vector

viktor.geometry.calculate_distance_vector(start_point, end_point)

Calculates the distance between start and end point in the direction start -> end.

Parameters:

start_point (Point) – Start position of the distance vector.
end_point (Point) – End position of the distance vector.

Return type:

ndarray

calculate_intersection_bounded_line_extended_line

viktor.geometry.calculate_intersection_bounded_line_extended_line(bounded_line, extended_line, inclusive=True)

Calculate intersection between line with fixed endpoints and line which is indefinitely extended.

Parameters:

bounded_line (Line) – Bounded Line object.
extended_line (Line) – Extended Line object.
inclusive (bool) – If set to True, this method will also check for end points that are located on one of the line ends.

Return type:

Optional[Point]

calculate_intersection_bounded_line_with_y

viktor.geometry.calculate_intersection_bounded_line_with_y(line, y_intersection)

Calculate x intersection between two points and y value. Return None if no intersection is found.

Returns x:                              Returns None:

        o
       /
y-----/---                              y---------
     /:                                      o
    / :                                     /
   o  x                                    o

Parameters:

line (Line) – Line object.
y_intersection (float) – y-value of the intersection line.

Return type:

Optional[float]

calculate_intersection_bounded_lines

viktor.geometry.calculate_intersection_bounded_lines(bounded_line1, bounded_line2, inclusive=True)

Calculate intersection between two lines with fixed endpoints (2D only, Z-coordinate is ignored!).

Parameters:

bounded_line1 (Line) – First bounded Line object.
bounded_line2 (Line) – Second bounded Line object.
inclusive (bool) – If set to True, intersections on the endpoint will also be taken into account.

Return type:

Optional[Point]

calculate_intersection_extended_line_with_x

viktor.geometry.calculate_intersection_extended_line_with_x(line, x)

Returns the point at which a given line intersects a vertical axis at position x.

Returns P(x, y):                        Returns P(x, y):

        o
       /
y-----P---                              y-----P----
     /:                                      o:
    / :                                     / :
   o  x                                    o  x

Parameters:

line (Line) – Line to be evaluated.
x (float) – x-value of the intersection line.

Return type:

Point

calculate_intersection_extended_line_with_y

viktor.geometry.calculate_intersection_extended_line_with_y(line, y_intersection)

Calculates the intersection x value of a line at a given y value.

Returns x:                              Returns x:

        o
       /
y-----/---                              y----------
     /:                                      o:
    / :                                     / :
   o  x                                    o  x

Parameters:

line (Line) – Line object.
y_intersection (float) – y-value of the intersection line.

Return type:

float

calculate_intersection_extended_lines

viktor.geometry.calculate_intersection_extended_lines(extended_line1, extended_line2)

Calculate intersection between two lines defined by start/end points. The lines are assumed to extend infinitely: bounds are not taken account. Returns None if lines are parallel (i.e. no intersection exists).

Returns P(x, y):                        Returns P(x, y):                        Returns None:

        o
       /
o-----P---o                             o--o P                                  o-----o
     /                                      o
    /                                      /                                    o--o
   o                                      o

Parameters:

extended_line1 (Line) – First Line object.
extended_line2 (Line) – Second Line object.

Return type:

Optional[Point]

cartesian_to_cylindrical

viktor.geometry.cartesian_to_cylindrical(cartesian_coordinates)

Using ISO convention: https://commons.wikimedia.org/wiki/File:Coord_system_CY_1.svg

Reference plane is former Cartesian xy-plane and cylindrical axis is the Cartesian z-axis.

Parameters:: cartesian_coordinates (Tuple[float, float, float]) – Cartesian coordinates (x, y, z).
Return type:: ndarray
Returns:: Cylindrical coordinates (rho, phi, z) with phi between -pi and +pi.

cartesian_to_spherical

viktor.geometry.cartesian_to_spherical(cartesian_coordinates)

Using ISO/physical convention: https://upload.wikimedia.org/wikipedia/commons/4/4f/3D_Spherical.svg

Parameters:: cartesian_coordinates (Tuple[float, float, float]) – Cartesian coordinates (x, y, z).
Return type:: ndarray
Returns:: Spherical coordinates (r, theta, phi).

circumference_is_clockwise

viktor.geometry.circumference_is_clockwise(circumference)

Method determines the direction of a set of points, and returns:

True if the circumference is clockwise
False if the circumference is counter-clockwise

Parameters:: circumference (List[Point]) – Circumference in x,y-plane.
Return type:: bool

convert_points_for_lathe

viktor.geometry.convert_points_for_lathe(points)

Method can be used to convert Point objects to lists of dictionaries in the format: {‘x’: point.x, ‘y’: point.y}

Parameters:: points (Sequence[Point]) – Point objects.
Return type:: List[dict]

cylindrical_to_cartesian

viktor.geometry.cylindrical_to_cartesian(cylindrical_coordinates)

Using ISO convention: https://commons.wikimedia.org/wiki/File:Coord_system_CY_1.svg

Reference plane is former Cartesian xy-plane and cylindrical axis is the Cartesian z-axis.

Parameters:: cylindrical_coordinates (Tuple[float, float, float]) – Cylindrical coordinates (rho, phi, z).
Return type:: ndarray
Returns:: Cartesian coordinates (x, y, z).

find_overlap

viktor.geometry.find_overlap(region_a, region_b, inclusive=False)

Given to regions with upper and lower boundary, check if there is overlap and if so return a tuple with the overlap found

The direction of the given regions does not matter: (1, 2) will be handled exactly the same as (2, 1) The returned Tuple will always be in ascending order

Example usage:

find_overlap((2, 4), (3, 5)) -> (3, 4)
find_overlap((4, 2), (5, 3)) -> (3, 4)
find_overlap((2, 3), (3, 4)) -> None
find_overlap((2, 3), (3, 4), inclusive=True) -> (3, 3)

Parameters:

region_a (Tuple[float, float]) – Tuple of values of the first region.
region_b (Tuple[float, float]) – Tuple of values of the second region.
inclusive (bool) – A flag to decide whether a point overlap is counted as overlap or not.

Return type:

Optional[Tuple[float, float]]

Returns:

A tuple with upper and lower bounds of the overlapping region, or None.

get_line_function_parameters

viktor.geometry.get_line_function_parameters(line)

Returns the line function parameters (a, b) of a line (y = ax + b).

Return type:: Tuple[float, float]

get_vertices_faces

viktor.geometry.get_vertices_faces(triangles)

Returns the vertices and faces of a list of Triangle objects.

Parameters:: triangles (List[Triangle]) – List of triangle objects.
Return type:: Tuple[list, list]

line_is_horizontal

viktor.geometry.line_is_horizontal(line)

Returns True if line is horizontal.

Return type:: bool

line_is_vertical

viktor.geometry.line_is_vertical(line)

Returns True if line is vertical.

Return type:: bool

lines_in_same_plane

viktor.geometry.lines_in_same_plane(line1, line2)

Method to determine whether two Line objects are located in a shared plane and hence are coplanar.

Parameters:

line1 (Line) – First line object.
line2 (Line) – Second line object.

Return type:

bool

mirror_object

viktor.geometry.mirror_object(obj, point, normal)

Function that mirrors an object through a plane. The plane is defined by a point and a normal vector. The return is a copy of the original object, mirrored over the specified plane.

Parameters:

obj (TransformableObject) – Object that is to be mirrored
point (Point) – Point object on the desired mirror plane
normal (Union[Vector, Tuple[float, float, float]]) – Vector that denotes a normal vector of the desired mirror plane.

Return type:

TransformableObject

point_is_on_bounded_line

viktor.geometry.point_is_on_bounded_line(point, line, inclusive=True)

Check whether a given Point object is within the ends of a Line.

Parameters:

point (Union[Point, Tuple[float, float, float]]) – Point to be evaluated.
line (Union[Line, Tuple[Tuple[float, float, float], Tuple[float, float, float]]]) – Line object.
inclusive (bool) – If True, this method will also return True when the point is located on one of the line ends.

Return type:

bool

points_are_coplanar

viktor.geometry.points_are_coplanar(points)

Determine whether all given points are coplanar (are on a two-dimensional plane).

Parameters:: points (Sequence[Union[Point, Tuple[float, float, float]]]) – points to be evaluated (min. 3).
Return type:: bool

Example usage:

points = [[Point(0, 3, 1), Point(0, 5, 1), Point(2, 3, 4), Point(2, 5, 4)]]
coplanar = points_are_coplanar(points)
coplanar = points_are_coplanar([(0, 3, 1), (0, 5, 1), (2, 3, 4), (2, 5, 4)])

reflection_matrix

viktor.geometry.reflection_matrix(point, normal)

Returns the reflection matrix to mirror at a plane defined by a point and a normal vector.

Parameters:

point (Union[Point, Tuple[float, float, float]]) – Point object.
normal (Union[Vector, Tuple[float, float, float]]) – Normal vector of the mirror plane.

Return type:

ndarray

rotation_matrix

viktor.geometry.rotation_matrix(angle, direction, point=None)

Returns the rotation matrix that corresponds to a rotation about an axis defined by a point and direction. Angle in radians, direction in accordance to right-hand rule.

Example:

R = rotation_matrix(pi/2, [0, 0, 1], [1, 0, 0])
np.allclose(np.dot(R, [0, 0, 0, 1]), [1, -1, 0, 1])  # True

Return type:: ndarray

scaling_matrix

viktor.geometry.scaling_matrix(scaling_vector)

Returns the scaling matrix that corresponds to a given scaling vector (3D).

Parameters:: scaling_vector (Union[Vector, Tuple[float, float, float]]) – Three-dimensional scaling vector.
Return type:: ndarray

spherical_to_cartesian

viktor.geometry.spherical_to_cartesian(spherical_coordinates)

Using ISO/physical convention: https://upload.wikimedia.org/wikipedia/commons/4/4f/3D_Spherical.svg

Parameters:: spherical_coordinates (Tuple[float, float, float]) – Spherical coordinates (r, theta, phi).
Return type:: ndarray
Returns:: Cartesian coordinates (x, y, z).

surface_area_dome

viktor.geometry.surface_area_dome(theta1, theta2, r, R)

Computes the surface area of a dome (arc-revolve).

Parameters:

theta1 (float) – Starting angle of arc in radians.
theta2 (float) – Ending angle of arc in radians.
r (float) – Radius of arc.
R (float) – Distance from centre of arc to rotation line.

Return type:

float

Returns:

surface area of arc-revolve.

surface_cone_without_base

viktor.geometry.surface_cone_without_base(r, h)

Calculates the exterior surface of the cone, excluding the area of the circular base.

Parameters:

r (float) – Radius of the base.
h (float) – Height of the cone.

Return type:

float

translation_matrix

viktor.geometry.translation_matrix(direction)

Returns the translation matrix that corresponds to a give direction vector (3D).

Parameters:: direction (Union[Vector, Tuple[float, float, float]]) – Direction vector of the translation.
Return type:: ndarray

unit_vector

viktor.geometry.unit_vector(data, axis=None, out=None)

Returns the unit vector of a given vector.

Return type:: Optional[ndarray]

volume_cone

viktor.geometry.volume_cone(r, h)

Calculates the volume of a cone.

Parameters:

r (float) – Radius of the base.
h (float) – Height of the cone.

Return type:

float

x_between_bounds

viktor.geometry.x_between_bounds(x, x1, x2, inclusive=True)

Method checks whether the x value is between the bounds x1 and x2.

Parameters:

x (float) – x-value to be evaluated.
x1 (float) – Lower bound.
x2 (float) – Upper bound.
inclusive (bool) – If set to True, this method will also return True when the x value is equal to either x1 or x2.

Return type:

bool

y_between_bounds

viktor.geometry.y_between_bounds(y, y1, y2, inclusive=True)

Method checks whether the y value is between the bounds y1 and y2.

Parameters:

y (float) – y-value to be evaluated.
y1 (float) – Lower bound.
y2 (float) – Upper bound.
inclusive (bool) – If set to True, this method will also return True when the y value is equal to either y1 or y2.

Return type:

bool

viktor.geometry

Arc​

ArcExtrusion​

ArcRevolve​

BidirectionalPattern​

CartesianAxes​

CircularExtrusion​

Cone​

Extrusion​

GeoPoint​

GeoPolygon​

GeoPolyline​

Group​

Line​

LineRevolve​

LinearPattern​

Material​

Pattern​

Point​

Polygon​

Polyline​

RDWGSConverter​

RectangularExtrusion​

Revolve​

Sphere​

SquareBeam​

Torus​

TransformableObject​

Triangle​

TriangleAssembly​

Vector​

add_point​

calculate_distance_vector​

calculate_intersection_bounded_line_extended_line​

calculate_intersection_bounded_line_with_y​

calculate_intersection_bounded_lines​

calculate_intersection_extended_line_with_x​

calculate_intersection_extended_line_with_y​

calculate_intersection_extended_lines​

cartesian_to_cylindrical​

cartesian_to_spherical​

circumference_is_clockwise​

convert_points_for_lathe​

cylindrical_to_cartesian​

find_overlap​

get_line_function_parameters​

get_vertices_faces​

line_is_horizontal​

line_is_vertical​

lines_in_same_plane​

mirror_object​

point_is_on_bounded_line​

points_are_coplanar​

reflection_matrix​

rotation_matrix​

scaling_matrix​

spherical_to_cartesian​

surface_area_dome​

surface_cone_without_base​

translation_matrix​

unit_vector​

volume_cone​

x_between_bounds​

y_between_bounds​

Arc

ArcExtrusion

ArcRevolve

BidirectionalPattern

CartesianAxes

CircularExtrusion

Cone

Extrusion

GeoPoint

GeoPolygon

GeoPolyline

Group

Line

LineRevolve

LinearPattern

Material

Pattern

Point

Polygon

Polyline

RDWGSConverter

RectangularExtrusion

Revolve

Sphere

SquareBeam

Torus

TransformableObject

Triangle

TriangleAssembly

Vector

add_point

calculate_distance_vector

calculate_intersection_bounded_line_extended_line

calculate_intersection_bounded_line_with_y

calculate_intersection_bounded_lines

calculate_intersection_extended_line_with_x

calculate_intersection_extended_line_with_y

calculate_intersection_extended_lines

cartesian_to_cylindrical

cartesian_to_spherical

circumference_is_clockwise

convert_points_for_lathe

cylindrical_to_cartesian

find_overlap

get_line_function_parameters

get_vertices_faces

line_is_horizontal

line_is_vertical

lines_in_same_plane

mirror_object

point_is_on_bounded_line

points_are_coplanar

reflection_matrix

rotation_matrix

scaling_matrix

spherical_to_cartesian

surface_area_dome

surface_cone_without_base

translation_matrix

unit_vector

volume_cone

x_between_bounds

y_between_bounds